Finding the Quantum Elevators
From Static Blueprint to Dynamic Action
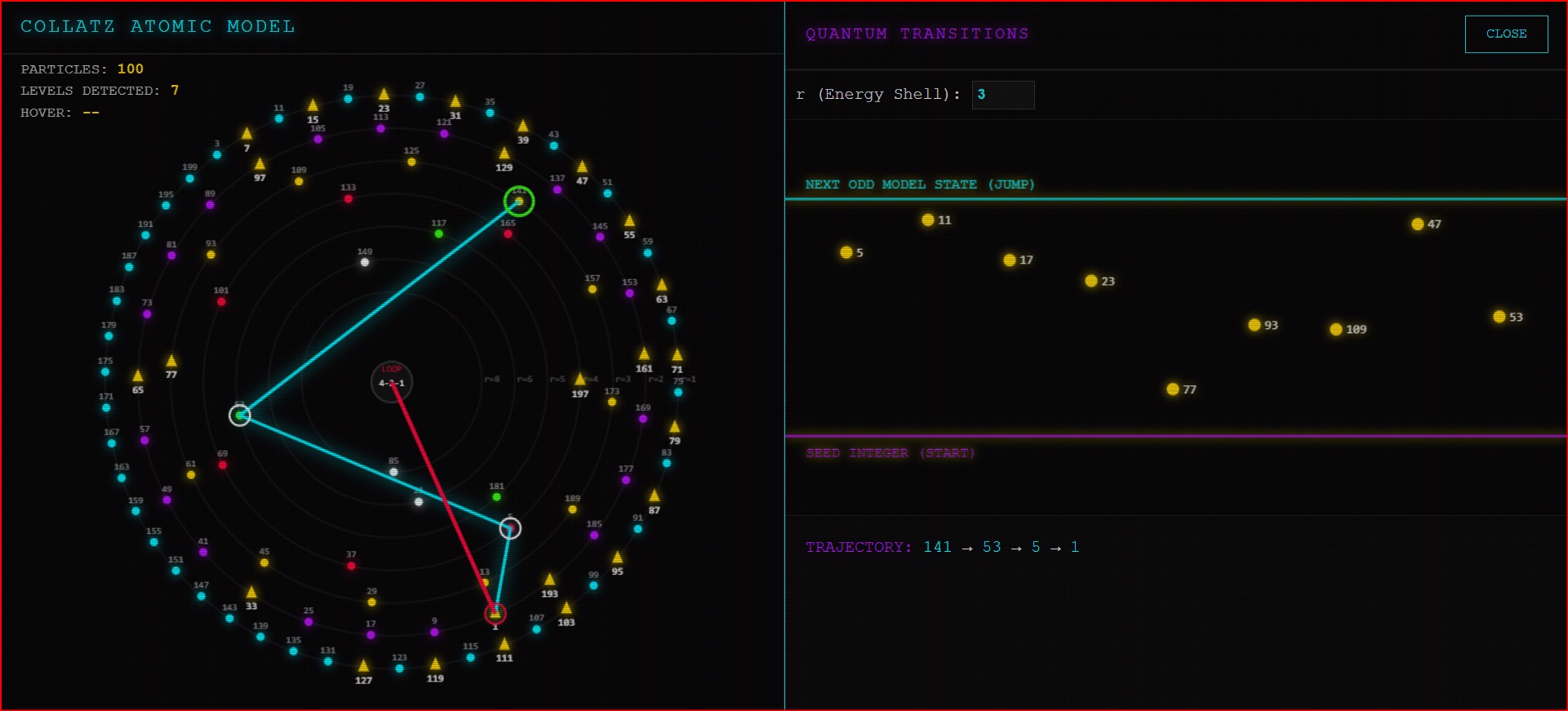
In the previous phase of our research (App #7), we achieved a fundamental breakthrough: we mapped the static anatomy of the integers. We discovered the Collatz Atomic Model, revealing that odd integers reside in discrete, quantized “energy shells” based on their Crash Power (r).
We had finally found the blueprint of the Collatz universe.
But a blueprint only tells you where things are, not how they move. The central mystery of the Collatz Conjecture is the wild, seemingly unpredictable movement of numbers between these shells.
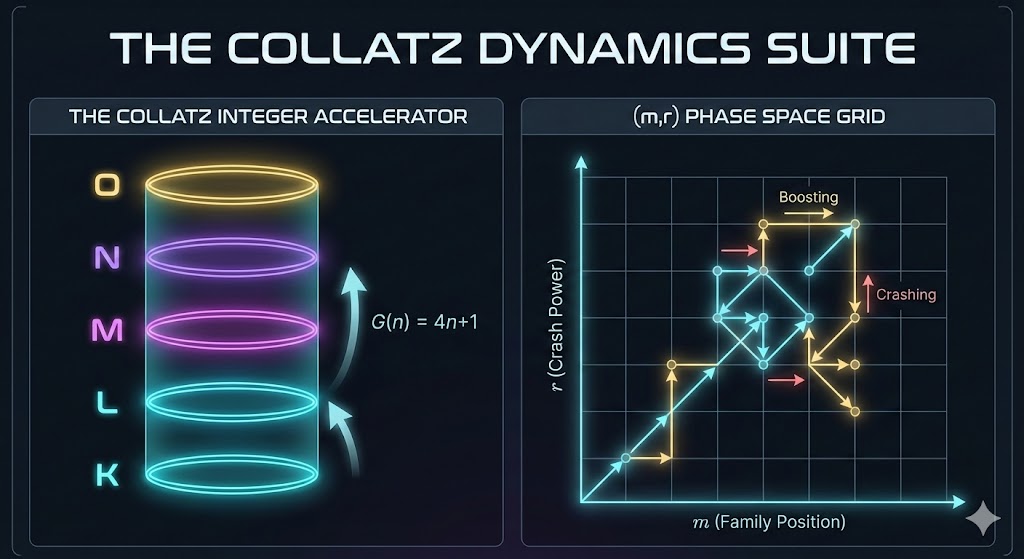
Today, I am releasing App #8: The Collatz Integer Accelerator. This new instrument is designed specifically to study this movement, moving us from a static view of structure to a dynamic understanding of action.
The Accelerator View
The primary view of this app is designed to test a specific hypothesis from my research paper: Are the jumps between energy shells always chaotic, or do deterministic pathways exist?
To test this, we isolate a powerful mathematical engine called the G-Operator:
G(n) = 4n + 1
This section visualizes what happens to an integer’s “atomic state” when we repeatedly hit it with this specific force.
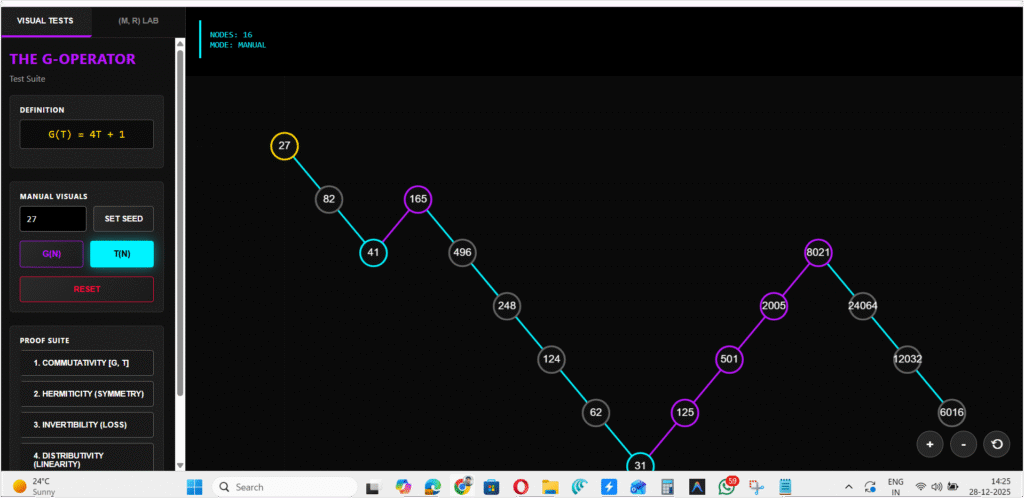
The Quantum Elevator
As the visualization proves, the result of this operator is not chaos. It is stunning, predictable order.
The G-Operator functions as a precision “quantum elevator.” Every time you apply the operator 4n+1 to an odd integer, you boost its position exactly two energy shells higher. A “ground state” integer (r=1) is deterministic boosted to shell r=3, then to shell r=5, and so on.
This proves that rigid, orderly pathways exist within the Collatz math.
The Map: The (m,r) Grid
We have identified a precise engine of movement. But in the real Collatz environment, this engine competes with the chaotic crashing forces of the standard 3n+1 rule.
To visualize this interaction, the second section of the app presents The (m,r) Grid.
This view visualizes the “phase space” of the odd integers. It places every integer on a 2D coordinate grid based on the parameters defined in my research (m on the X-axis, r on the Y-axis).
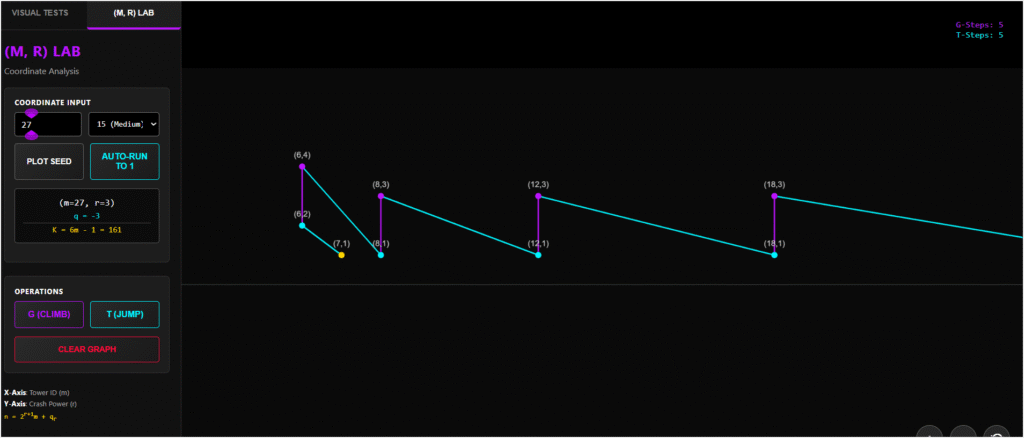
Visualizing the Tug-of-War
This grid is the game board where the forces of arithmetic battle it out. By navigating this grid, you can witness the fundamental tension of the Collatz problem.
You can see the Accelerator (G-Operator) trying to boost the integer systematically up the Y-axis to higher structures, while the standard Collatz rules (Force of Chaos) intervene, crashing the trajectory back down toward the “ground state” at the bottom of the grid.
A Collatz trajectory is no longer just a squiggly line; it is a traceable path through a highly structured 2D landscape.
Conclusion
With the release of The Collatz Integer Accelerator, our toolkit has evolved significantly. We have moved from observing chaotic flights to mapping the atomic structure, and now, to discovering deterministic engines and visualizing the entire interactive phase space.
We are no longer looking at random noise. We are looking at a complex, structured system whose rules we are finally beginning to see.