Visualizing the Decoherence of Arithmetic Linearity
From Mapping to Measuring
In the previous posts of this series, we focused on Mapping the Collatz Conjecture. We built the Collatz Periodic Table (App 4) to classify integers into “Crash Families” (r) and assign them unique coordinates. We organized the chaos.
But as any physicist knows, drawing a map is only the first step. To truly understand a system, you have to break it apart and measure the pieces. You need an instrument.
Today, I am releasing App #5: The Collatz Interferometer.
The Theory: Arithmetic as a Beam of Light
In optics, an Interferometer splits a beam of light into two paths. If the paths stay in sync (phase), they recombine perfectly. If they drift apart, you get an “interference pattern” that reveals hidden defects in the medium.
My research proposes that odd integers behave exactly like these light beams.
Specifically, odd integers can be written in the form N = ODD + EVEN = (2n+1) + 2n and they possess a unique internal structure. They are not atomic; they are composite.
The interest here is to see, when a Collatz operator acts linearly on these components will the system behave linearly
i.e can T(4n+1) = T(2n) + T(2n+1) and if so for which integers will this relationship hold good
But when the “parity phase” mismatches, this linearity decoheres. The equation breaks, and the system spirals into chaos.
The Tool: The Non-Linearity Lab
I built this app to let you watch this “Arithmetic Decoherence” happen in real-time. The Collatz Interferometer
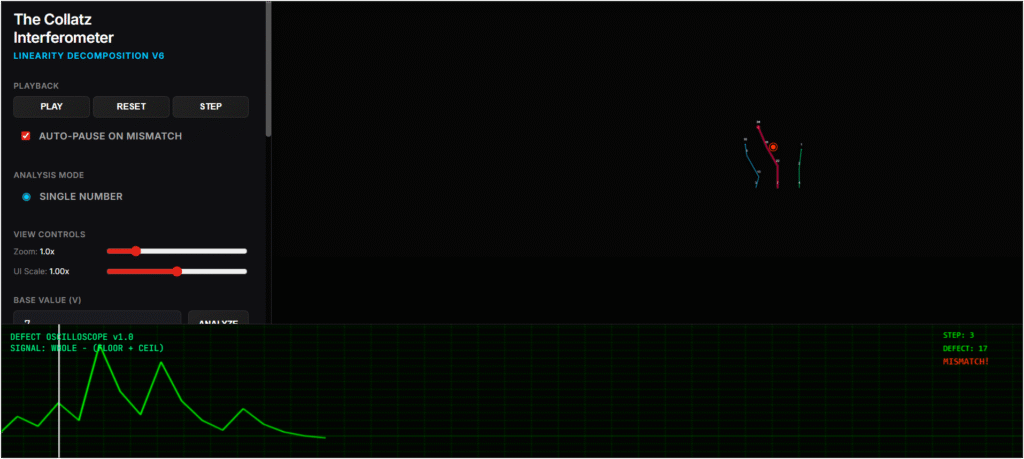
How to Read the Data
This app is a precision instrument. Here is what you are looking at:
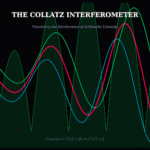
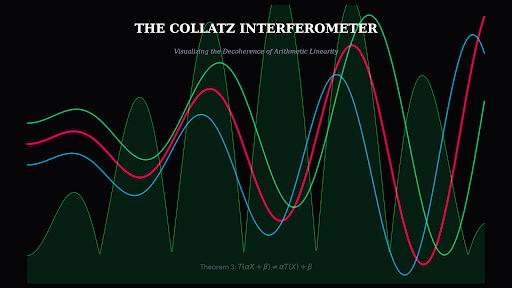
1. The Beam Splitter (The Ribbons)
- Red Ribbon (4n+1): This is the trajectory of the whole number.
- Cyan & Green Ribbons (2n, 2n+1): These are the decomposed parts.
- The Experiment: Watch them flow. Do they stay parallel (Linear)? Or do they violently diverge (Non-Linear)?
2. The Defect Oscilloscope (Bottom Panel)
Physics is about error analysis. The Green Oscilloscope at the bottom measures the “Linearity Defect”:
Linearity Defect = T(N) – T(2n) – T(2n+1)
- Flat Line: The system is perfectly linear. The arithmetic is stable.
- Spike: A “Non-Linear Event” has occurred. The integer has hit a parity wall that shattered its internal structure.
Why This Matters
We often think of numbers as static points on a line. This tool proves they are dynamic systems with internal “moving parts.” By treating the Collatz Conjecture as a problem of Linearity Breaking rather than just a random walk, we get closer to understanding why it never diverges to infinity.
The Interferometer reveals that the “Chaos” of the Collatz problem isn’t random noise—it is simply the interference pattern of broken symmetries.