Collatz Conjecture: – 7 The Collatz Atomic Model

The Anatomy of Integers

From Dynamics to Structure

For the first six installments of this research series, we have been obsessed with the motion of the Collatz Conjecture. We have built instruments to track the chaotic trajectories, measure their dizzying heights, and time their eventual decay. We have studied the dynamics of the problem.

But looking at the flight path of a bird tells you little about its biology. To truly understand the complex reactions of the Collatz problem, we first need to understand the fundamental structure of the “atoms” themselves.

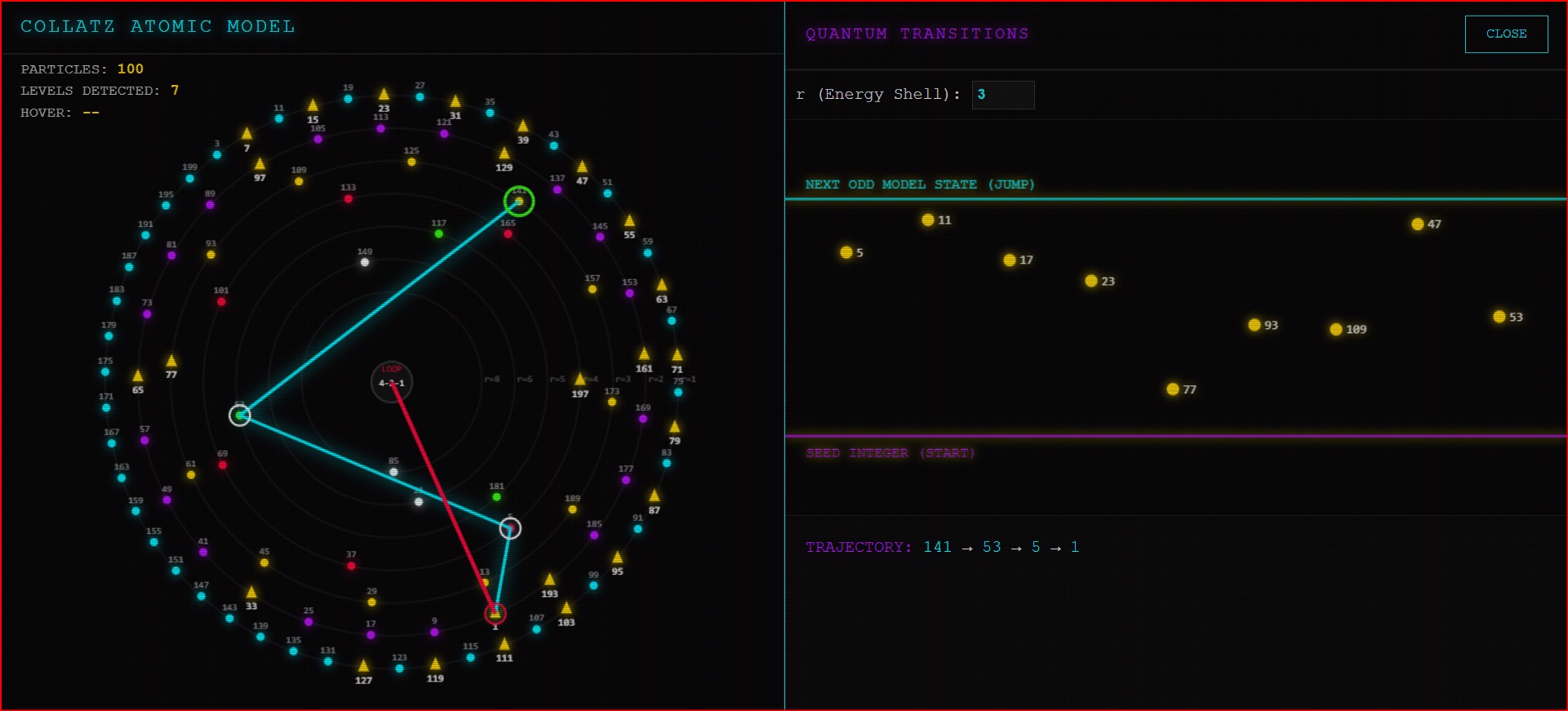
Today, I am releasing App #7: The Collatz Atomic Model.

This visualization marks a pivotal shift in our journey. It is not about what the numbers do; it is a blueprint of what they are. We are moving from observing chaos to revealing structure.

The Bohr Analogy: Quantized Integer Shells

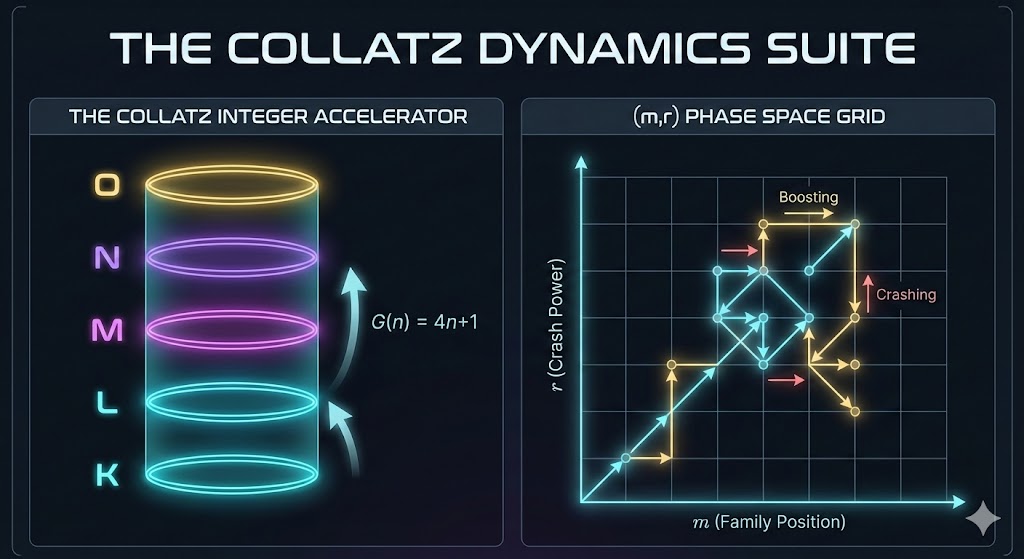
In the early 20th century, the Bohr model revolutionized physics by proposing that electrons within an atom cannot exist just anywhere. They must occupy discrete, quantized energy shells (labeled K, L, M, N, O…).

My research proposes a direct mathematical parallel for odd integers in the Collatz universe.

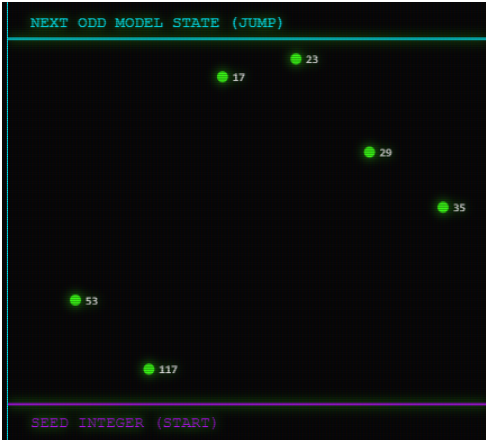
An integer cannot just have any random arithmetic property. Its behavior in the very first step of the Collatz function is rigidly determined by its “Crash Power” (r)—which is the number of times the odd integer is divided by 2 in a single step.

This app visualizes these arithmetic properties not as a list, but as quantized physical shells.

As you explore the model, you will see that every odd integer belongs to exactly one of these discrete shells, determined by the rigorous arithmetic rules of my research.

Decoding the Atomic Map: A Guide to the Legends

Just as a periodic table requires a legend to be understood, the Collatz Atomic Model uses a specific visual language to map the territory. Here is how to interpret what you are seeing:

1. The Quantized Shells (K, L, M…)

These labels, borrowed directly from electron shell notation in physics, represent the Principal Energy Levels of the integers based on their Crash Power (r).

• K-Shell (r=1): The “Ground State.” Contains the vast majority of integers that divide by 2 only once (e.g., 3, 7, 11).
• L-Shell (r=2): The first excited state. Integers that divide by 4 (e.g., 1, 5, 9).
• M, N, O…: Higher states representing increasingly rare arithmetic families (r=3, 4, 5…).

2. The Color Spectra

To visually distinguish the energy levels, each shell is assigned a distinct neon color consistent with the themes used throughout this research series (Cyan for ground state, Purple for r=2, etc.).

3. The Transition Triangles (Intra-Orbit Markers)

Perhaps the most intriguing feature for advanced observers are the small triangular markers placed on specific integers within the orbits.

While the primary drama of the Collatz Conjecture involves numbers jumping between different shells (e.g., from K to N), these triangles indicate critical arithmetic transitions occurring within the same orbit itself. They mark special numbers representing internal turning points or sub-structures within a single stable family.

Precision over Uncertainty: The Limits of the Analogy

While the visual parallel to Bohr’s model is striking, as researchers, we must define the boundaries of this analogy. Based on my observations in building this model, there are key differences between physical atoms and our mathematical ones:

a. The Triumph over Heisenberg

In quantum mechanics, the Heisenberg Uncertainty Principle dictates that we cannot precisely know both the position and momentum of an electron. Its location is probabilistic.

In our mathematical model, there is no such uncertainty. Because every integer is governed by strict arithmetic rules, an integer’s position in its orbit is precisely defined by its unique coordinate pair (n, r). Unlike a fuzzy electron, we know exactly where every number lives in the Collatz universe.

b. Structure, Not Emission (Yet)

In real atoms, when an electron jumps from a high shell to a lower one, it emits a photon (energy/light). In this current iteration of the Collatz Atomic Model, transitions between shells do not “emit” anything. This model is currently a static structural analogy intended to map positions, not a functional one describing energy transfer.

(Note: You will also notice adjacent orbits rotating in opposite directions. This is an arbitrary visual choice intended to emphasize that each shell is a distinct, self-contained system.)

Conclusion: The Skeleton of Chaos

The Collatz Atomic Model gives us a necessary, static view of a dynamic problem.

It proves that the “chaos” of Collatz trajectories is not happening in a vacuum. It is playing out upon a rigid, highly organized, quantized skeleton. Before we can fully understand the unpredictable jumps from shell to shell, we must first understand the precise structure of the shells themselves.