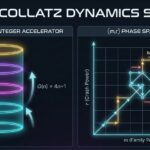
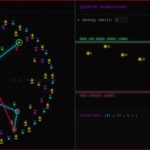
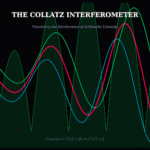
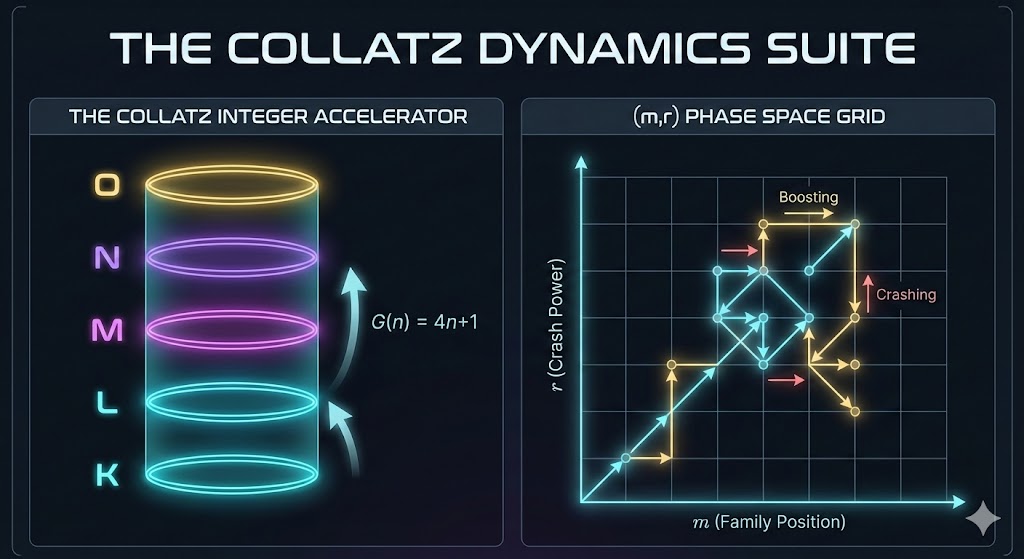
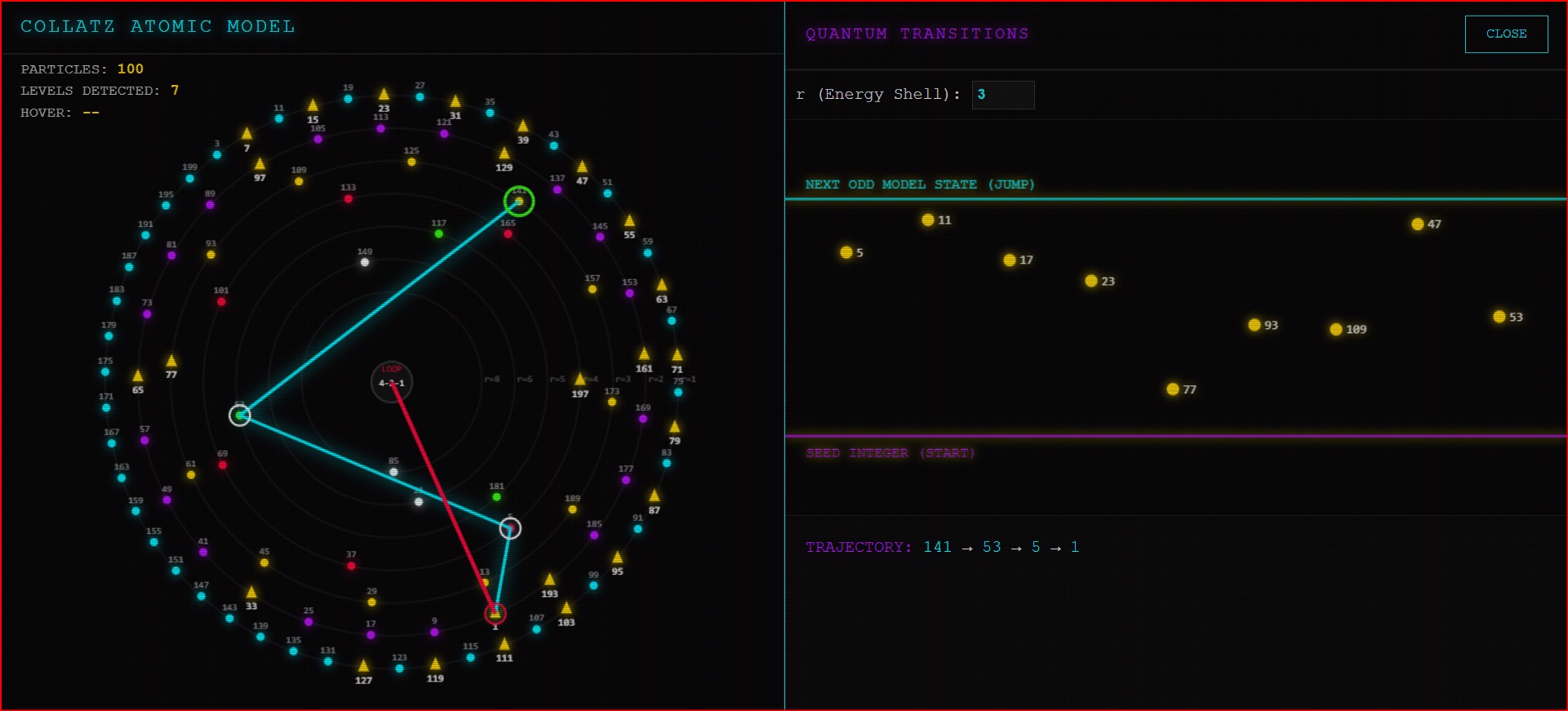
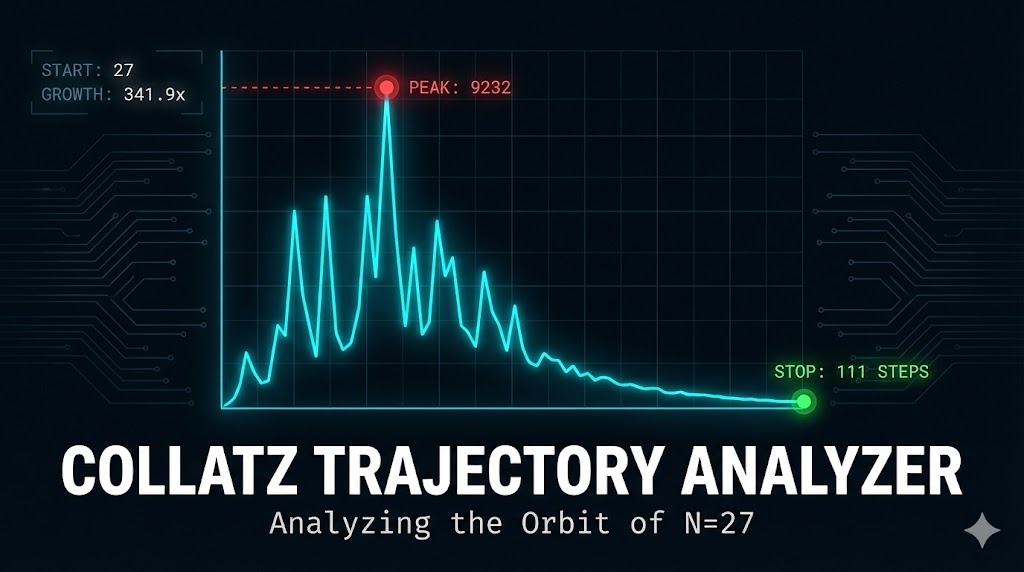
In my last few posts, we looked at the “loops” of the Collatz problem. We saw how positive numbers get stuck in the 4-2-1 loop, and how negative numbers have their own hidden loops in a “mirror world.”
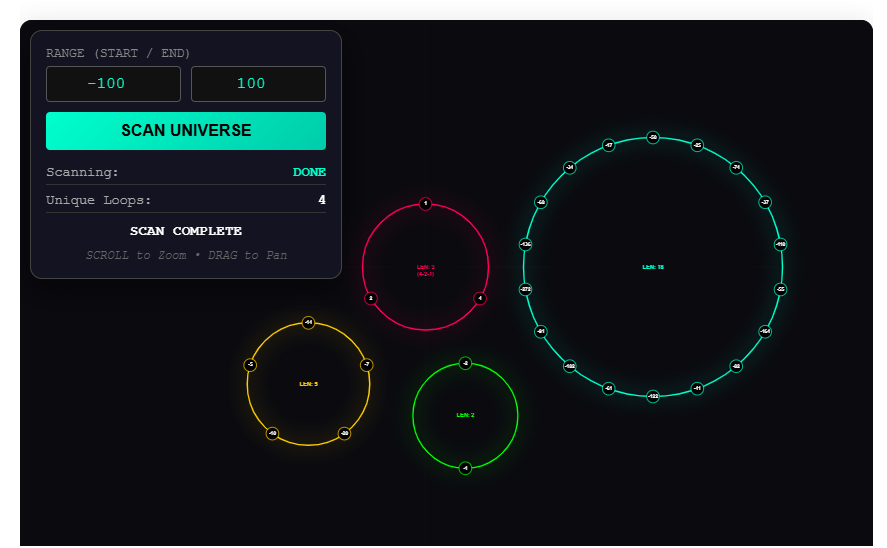
In the next post, I created an app that displayed how the collatz iterates can be obtained for any integer. You can click the below image to access that app.
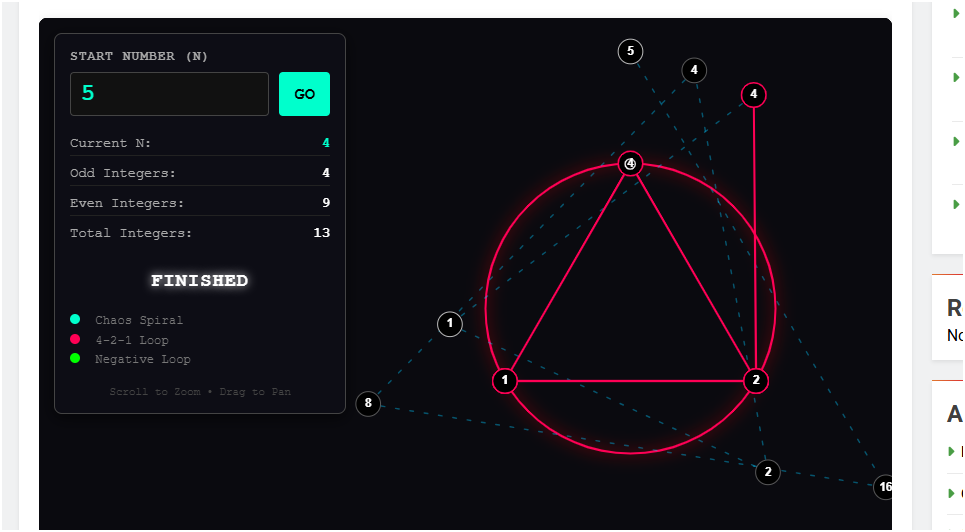
But recently, I started thinking about the journey itself.
When you write down a sequence—like 27, 82, 41, 124…—it just looks like a random mess of numbers. But as a physicist, I know that “messy” data often hides beautiful patterns if you look at it the right way.
The Physics of Chaos
Think about things we see in nature:
- The Weather: Temperature numbers look random on a page. But if you plot them out like Edward Lorenz did, that chaos turns into a perfect, butterfly-shaped pattern.
- Rivers: A rushing river looks like random splashes. But physics tells us those splashes are actually organized whirlpools.
- Snowflakes: Water molecules move randomly. But when it gets cold, they lock together into perfect six-sided crystals.
I realized I needed to treat the Collatz problem like a physics experiment. So, I used a tool called Antigravity to do some “Vibe Coding.” I built a new app called the Collatz Fractal Gallery.
This app lets us stop calculating numbers and start seeing them. Here is what I found.
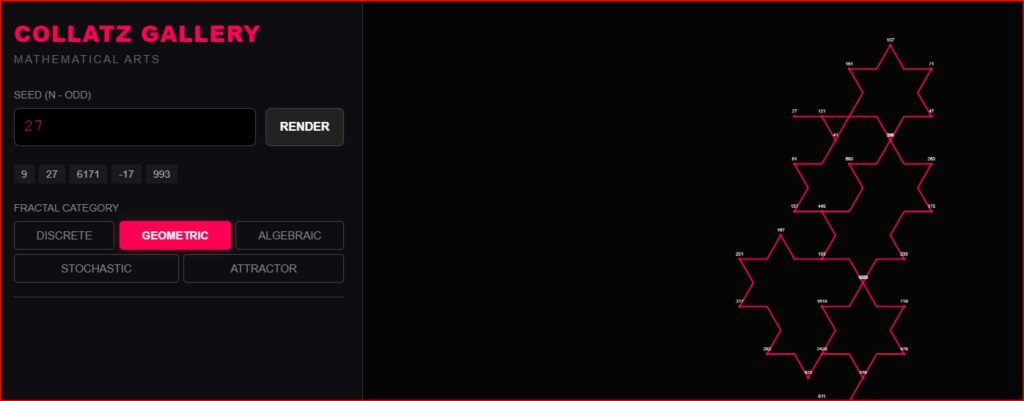
1. The Snowflake Effect
In physics, simple rules create complex shapes. I tried applying this to the Collatz numbers using something called “Turtle Graphics”.
- The Rule: If the number grows (3n+1), the pen moves forward. If it shrinks (divide by 2), the pen turns 60 degrees.
I thought it would look like a scribble. Instead, I got snowflakes.
Numbers like 27 don’t just wander around; they fold in on themselves to create beautiful, organic shapes. The app shows us that specific numbers make the path do a complete U-turn, creating perfect symmetry.
2. Is it Random? (The Coin Flip Test)
Students often ask me, “Is the Collatz sequence just random?”
It definitely looks random. So, I built a “Stochastic Mode” to test it. The app draws two lines:
- Red Line: The actual Collatz path.
- White Line: A path where every step is just a random 50/50 coin flip.
The difference is huge. The White line wanders off aimlessly, sometimes drifting up forever. But the Red line, even with its wild spikes, feels like it has “gravity.” It is eventually pulled down to 1. It proves this isn’t random noise—it is chaos with a destination.
3. The Trap
In mechanics, we use graphs to track moving systems. I did the same here using a “Phase Plot”.
I plotted the current number against the next number. When the numbers are flying around, the dots are everywhere. But the moment the sequence hits a loop, the dots snap into a rigid geometric shape—usually a triangle. You can actually see the number getting “trapped” by the logic.
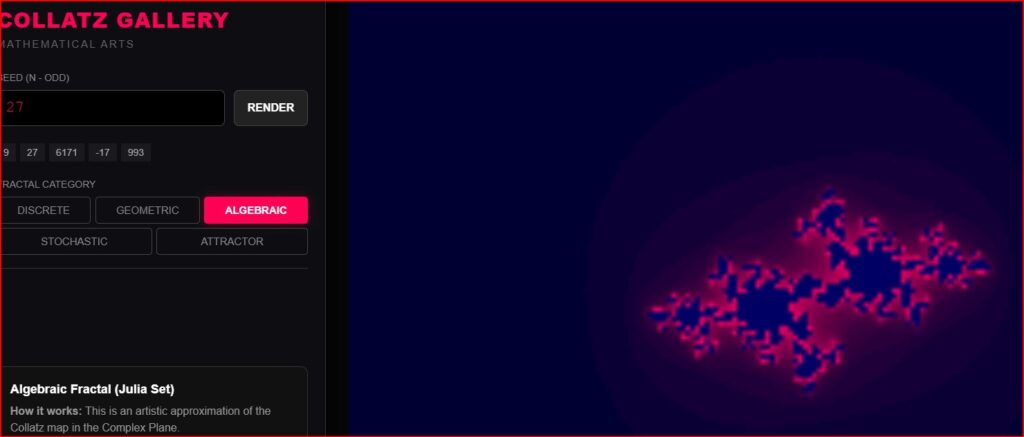
Why “Antigravity” Matters
I have been working on this problem since 1996. Back then, I only had graph paper. Today, I use Antigravity to generate these visuals in seconds.
I am not a professional coder. I didn’t write the complex rendering code for this myself. But I have the intuition for how the numbers should behave. By guiding Antigravity with the logic, I could build a tool that helps us see the math in a completely new way.
Try the Gallery available at https://prayogashaala.com/collatz-fractals/
I have uploaded this simulation to my website. You can switch between the “Geometric,” “Algebraic,” and “Stochastic” views to see the hidden structure for yourself.
Does the number 993 look like a snowflake or a storm? Go find out.