In Parts 1, 2, and 3, we treated the Collatz Conjecture like a movie—we watched numbers travel through loops, spirals, and fractals. We were observers of the chaos.
But as a physicist, observation isn’t enough. We need classification.
Before Mendeleev created the Periodic Table, chemistry was a messy list of elements. Mendeleev realized that elements repeat their behaviors in predictable cycles.
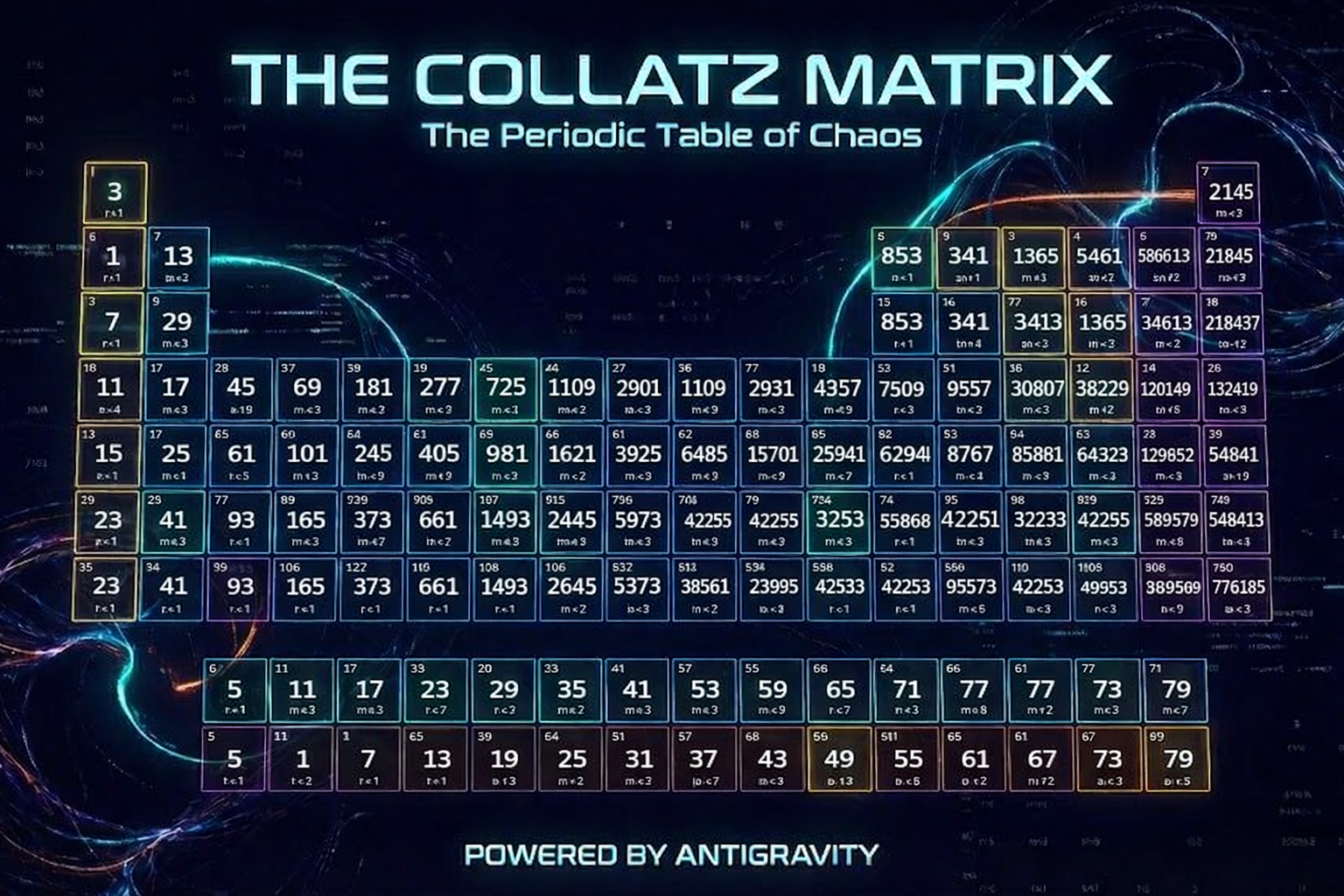
I realized the odd numbers in the Collatz universe do the same thing. So, I used Antigravity to build the Collatz Classification Matrix.
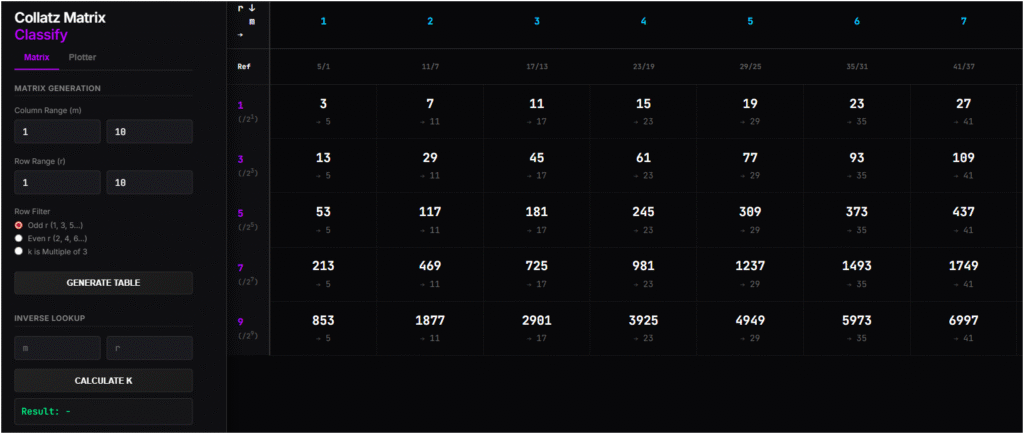
The Hidden Hierarchy
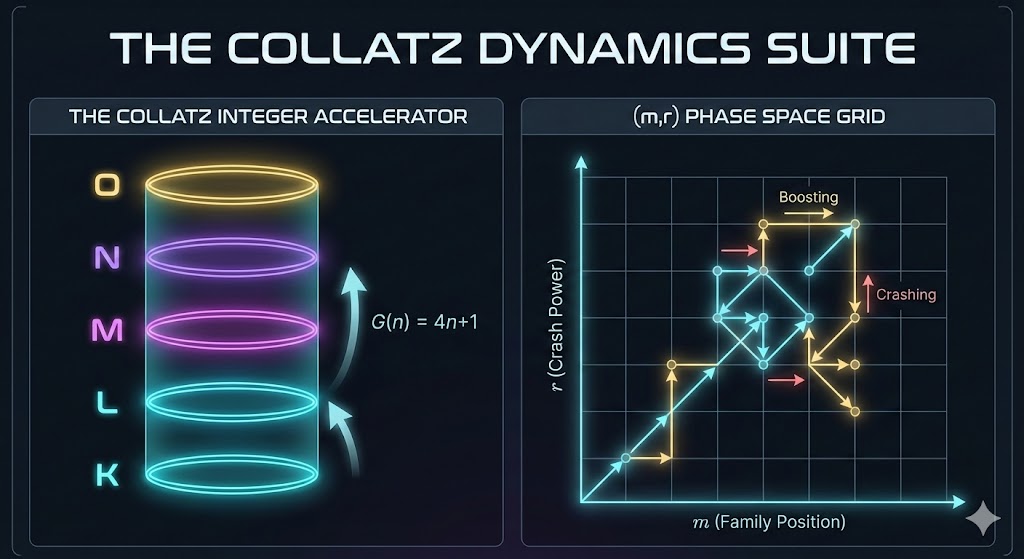
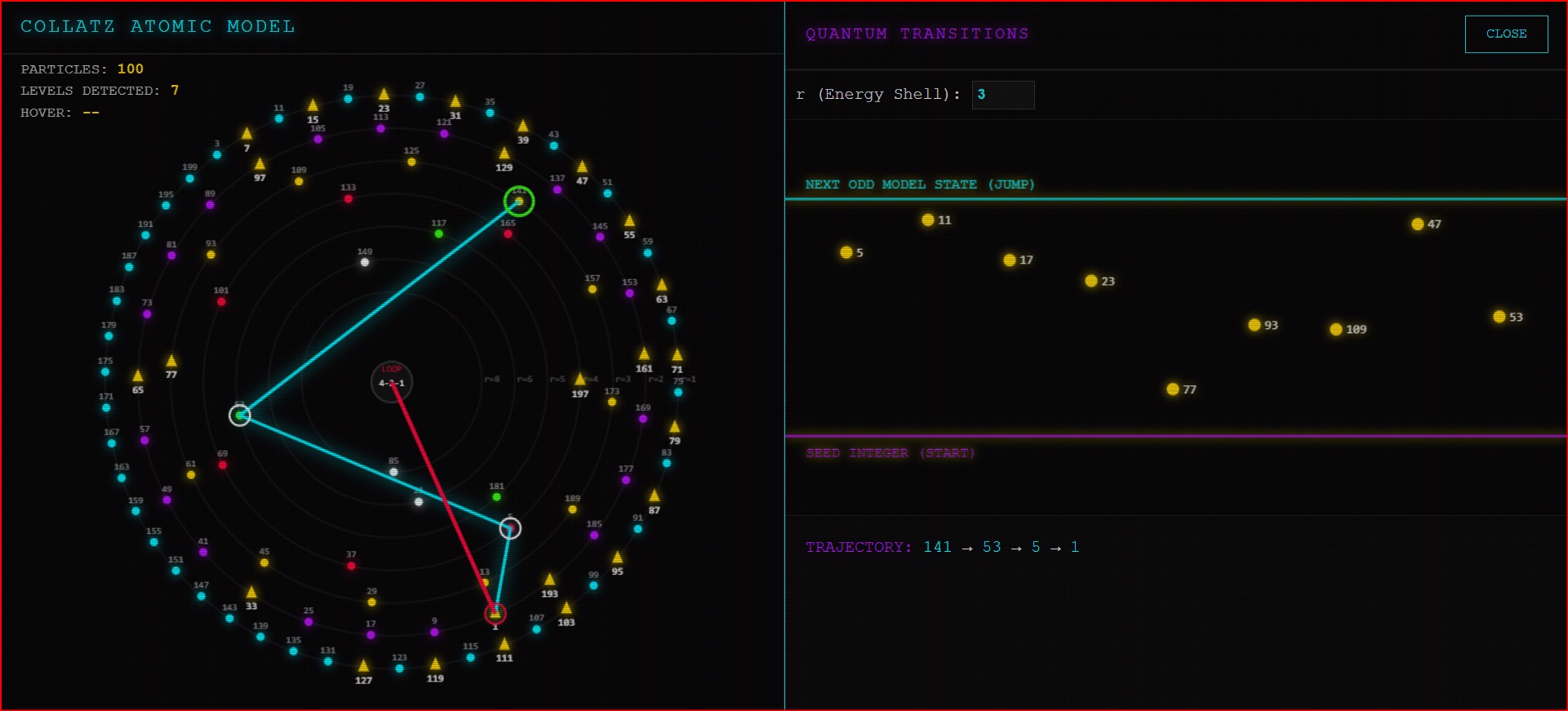
When you take an odd number n and apply 3n+1, the result is always even. The big question is: How even is it?
- Does it divide by 2 just once? (A small dip, r=1)
- Does it divide by 32? (A massive crash, r=5)
We usually think this is random. It is not.
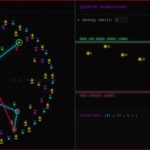
Using this tool, I organized the odd integers into a Matrix where:
- Rows (r): Represent the “Crash Power” (how many times we divide by 2).
- Columns (m): Represent the “Family Index.”
Why Odd Multiples of 3 are Special
One of the most important filters I built into this tool is for Odd Multiples of 3 (3, 9, 15, 21…).
Why focus on them?
In the Collatz rule (3n+1), the collatz iterates always form an odd integer which is of the form 6m-1 or 6m-5 and hence the result can never be a multiple of 3.
This means odd multiples of 3 are the “Orphans” of the Collatz graph. No odd number can ever grow into them. They are the starting points—the “leaves” of the tree.
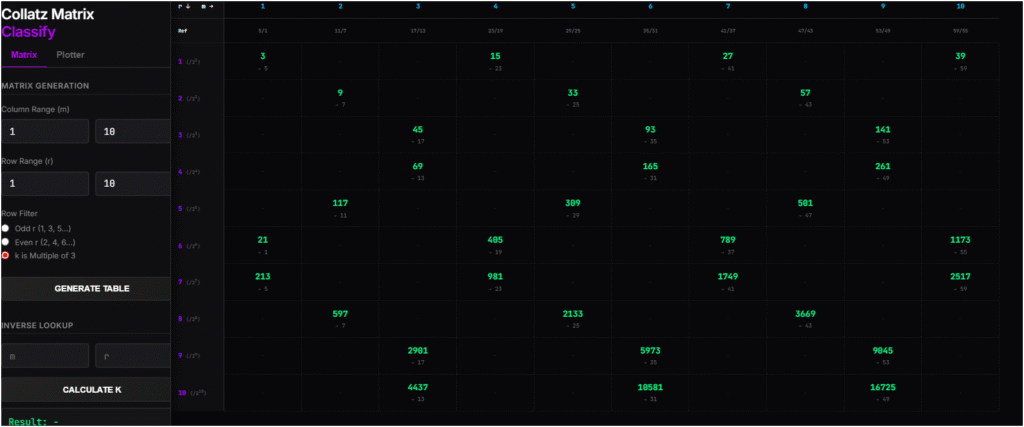
By filtering for these specific numbers in the Matrix, we can analyze if these “Garden of Eden” numbers share a specific crash DNA compared to the rest of the number line.
Plotting Primes & Fibonacci: Searching for Structure
This tool also includes a Series Plotter. It allows you to map specific sequences—like Prime Numbers or Fibonacci Numbers—onto the Collatz coordinates.
Why do this?
We know Prime numbers are the “atoms” of arithmetic. We know Fibonacci represents organic growth in nature. Collatz, on the other hand, represents chaotic growth.
- Does the chaos of 3n+1 respect the order of Primes?
- Do Fibonacci numbers cluster in specific “crash rows”?
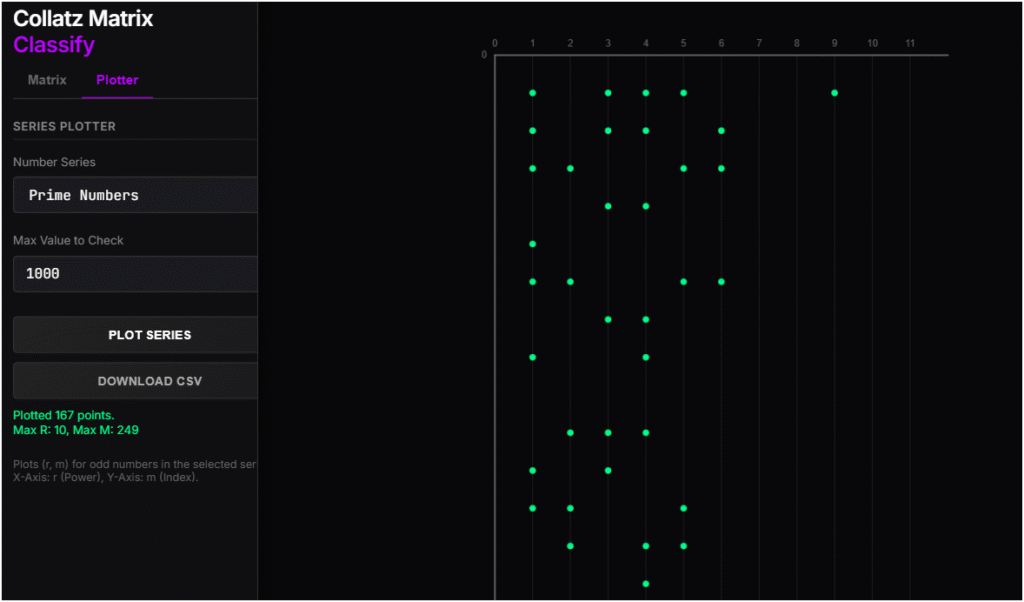
By visualizing these series on the (r, m) graph, we aren’t just looking at random points. We are looking for correlations between the fundamental structures of mathematics and the chaotic Collatz map.
Explore the Matrix
I have uploaded the tool below.
- Use the “Filter” to isolate Odd Multiples of 3 and see where they live.
- Switch to the “Plotter” tab to visualize where Prime Numbers hide in the Collatz landscape.
- Download your data as a CSV to analyze the patterns yourself.
Link to Collatz Classification Matrix: https://prayogashaala.com/collatz-matrix/




Great work…good start
Thank you